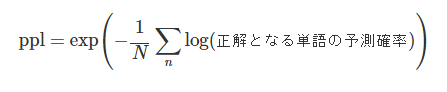先に結論
- 研究自体は素晴らしい内容
- フェーズとしては、応用というより基礎に近く、すぐに活用されることはなさそう。1-2年後、あるいはさらに先になる可能性もありそう
このような結論になった理由について、記事内で触れていきます!
BitNetの事前研究
まず、混乱を避けるためにあえて触れますが、BitNetの論文は2つ公開されています。
・2023年10月【BitNet】
・2024年2月【BitNet b1.58】
今回扱うのは後者のb1.58です
単純にBitNetと検索するだけだと、前者がヒットしてしまう場合があるためご注意ください🍜
BitNet b1.58の概要
公式の論文の図を日本語説明にしました!
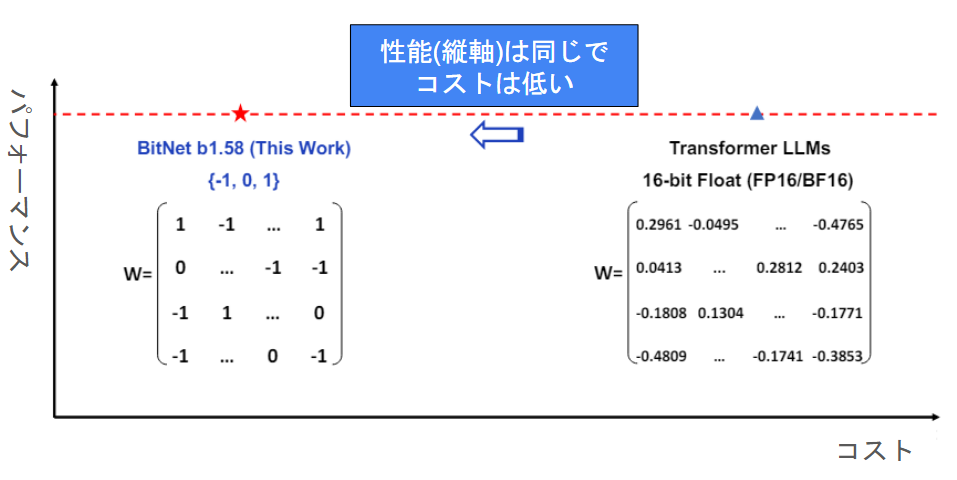
従来のTransformerが右側にあり、それよりも
- コストは小さくシフト
- 精度は維持
というのを主張しています。
最高精度達成!というよりは、GPU高価すぎるのでランニングコスト抑えましょうね、という発表です!🍞
具体的には、以下の新しい構造でもって計算を行います。
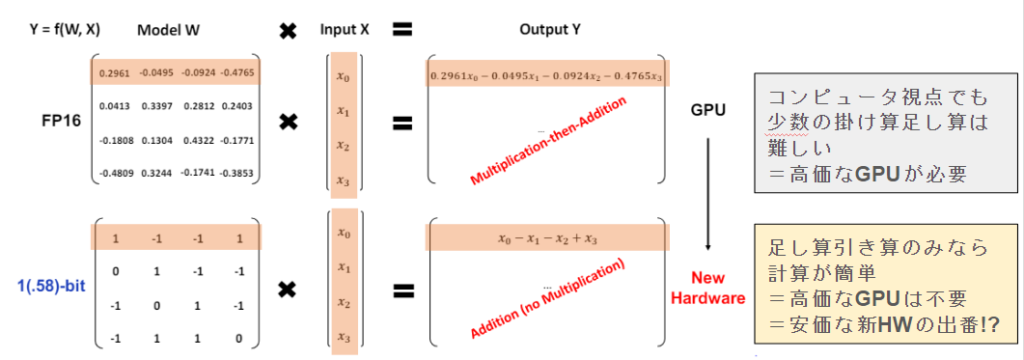
従来は、fp16という少数で計算していた部分を、[+1, 0, -1]のみにかえるみたいです。
従来は
「0.2961 × x0」を計算していた部分が単に「x0」になっており、+1, -1というより符号が、正か負か0か、くらいに考えたほうがよさそうですね♪
効果のほどは?
効率性
論文には以下の表のようになっています!
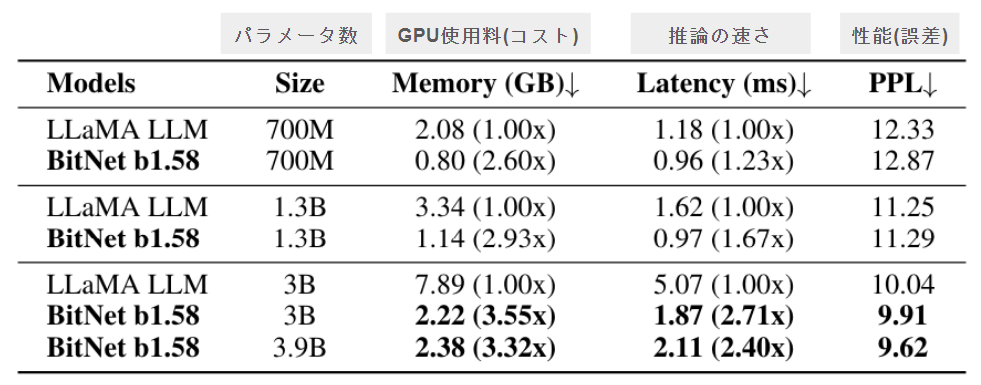
同じサイズ感のLLaMAのモデルと比較して、
- GPUは2.6倍~3.55倍効率的(少ないGPU)で推論可能
- 推論は1.23倍~2.71倍高速に推論可能
- PPL(簡易な性能指標)はBitNetのほうが良い結果
という形になています。
PPLについてはこちらの記事から表現を引用させていただきます。
https://data-analytics.fun/2022/01/15/understanding-perplexity/
誤差のような意味合いで解釈するのが良いかなと思います!
精度
公式の論文で報告されている精度です!
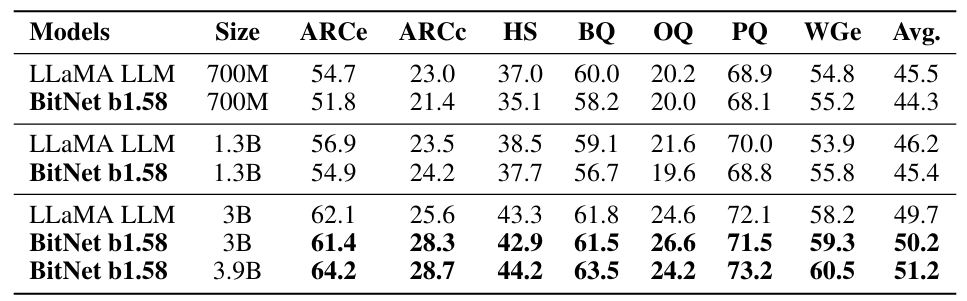
およそ、Llamaと似たような精度になっていますね。
なお、このベンチマークは、lm-evaluation-harnessで評価しており、hugging faceでもリーダーボードが公開されています。
3B以下のLLMの評価。ARCは66-68、HSは85程度になっています。
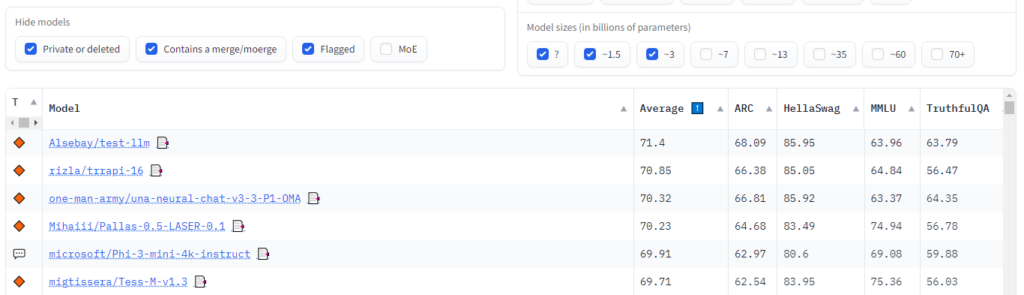

あと、恐らくですが、このLlamaは、公開されているモデルの重みLlamaではなく、LlamaのアーキテクチャとBitNetのアーキテクチャで比較していて、学習データは同じなのではないかなと推測しています。
メッセージとしては、あくまで”匹敵する”レベルという形でしょうか。同じ3B帯の中で優秀な精度、というわけではなさそうです。ただ、これはMeta社の持つデータの影響もありえます。
エネルギー
論文でもエネルギー効率が良いことが触れられてます。
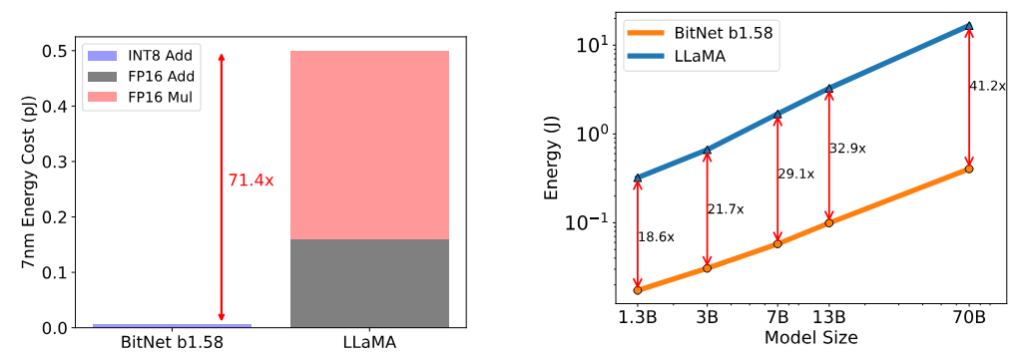
エネルギー効率も大事なことではありますが、世の現状としては高精度なLLMの活用から、という状況かなと思います。その点でもこのエネルギー効率化は中長期の研究よりのテーマであります。
もう少し詳しい内部挙動について
1本目の論文の図で理解は十分かなと思います。
DeepLearningの基本演算子であるLinear層をBitLinearに置き換えるだけです。このBitLinearの中に、1-bit Weightsがありますね!
Linear層というのはよくあるこういうやつです。
このBitLinearが、TransformerのLinearがあった部分に変わりに使われています。割とシンプルですね!
なお、1.58bitというのは、この従来の[-1, +1]からなる「1-bit Wights」の部分を[-1, 0, +1]の3値になる「1.58bit Weights」になるのが最新論文です!🔥
なんで、1.58bit?
bitというのは2進数のことで以下の表のようになります。
| bit演算 | 2進数の値 | 2進数 | 表現できる値の数 |
| 1bit | 0~1 | 2^1 | 2 |
| 2bit | 00~11 | 2^2 | 4 |
| 3bit | 000~111 | 2^3 | 8 |
従来のBitNetは、[-1, +1]の二値で表現していたため、1bitのLLMでした。
一方最新論文のBitNet b1.58では、[+1, 0, -1]の三値で表現します。このため、1bitと2bitの間の1.58bitになるようです。
厳密には、3個の値である[+1, 0, -1]のエントロピーを計算するそうです。
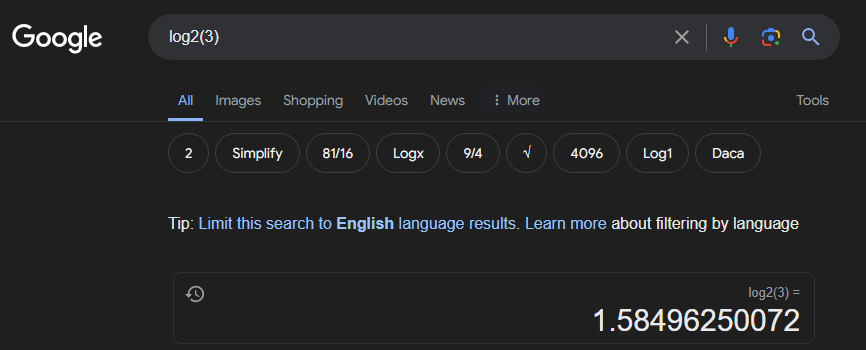
だから1.58bitなんですね♪
実装上の工夫(誤差逆伝搬)
DeepLearning系やったことがある人向けの解説です。
この量子化、整数化というのは素敵そうに見えて実際には学習できません。
誤差逆伝搬とAIの学習(重みの更新)というのは、以下のイメージで処理をします。

一方、BitNetの場合は、少しずつ答えを合わせこむというのができません。

AIの基本の考え方として、学習の段階から[+1, -1]といったビット演算で処理をするのは、そもそも出来ないことで、工夫やトリックが必要です。
この点は面白い実装方法をしていて、Pythonスクリプトそのものが参考になります。
class BitLinear(nn.Linear):
def forward(self, x: Tensor) -> Tensor:
# w = モデルの重み
w = self.weight
# 入力データxの正規化
x_norm = SimpleRMSNorm(self.in_features)(x)
# 入力データの軽い量子化(8bit)
x_quant = x_norm + (activation_quant(x_norm) - x_norm).detach()
# モデルの重みの2値化
w_quant = w + (weight_quant(w) - w).detach()
# この量子化された重みで計算
y = F.linear(x_quant, w_quant)
return yこのうち、面白いところはここです。
w_quant = w + (weight_quant(w) - w).detach()w_quantは結局のところ、wに、(量子化w)を足して、wを引いてます。
wを足してwを引くんですよね。
これは、先ほどの通り「量子化したパラメータは学習できない」という都合です。そのため、この計算では
| weight_quant(w) | 非連続で学習できない |
| (weight_quant(w) – w).detach() | 非連続で学習できない |
| w | 元の小数値のパラメータは学習できる |
| w + (weight_quant(w) – w).detach() | 右側は学習できないが、左項のwは学習可能 |
こういう形で、計算にはw_quantを使うが、バックワードはwにするというトリックが使われて学習されています。
ここは私がこの論文のファーストインプレッションでとても気になっていたことで、今回の記事にともなって調べることで知れてよかったです🧡
BitNet 1.58Bの注意事項
“新しいハードウェア”というのは現状まだ存在しない
GPUが乗算が得意なパラメータである一方で、BitNetは足し算引き算で演算できますよ、という強みを持ちます。GPUの次の世代の推論ハードがあることで真の価値を発揮する場合もあります。
なぜか公式実装が公開されていない
そもそもの実装の難易度が高いこともあり、公式から実装方法を公開してほしいですね
検証が3Bまでしか行われていない
BitNet b1.58の論文では、3Bまでは精度検証が報告されていますが、逆に言うと3Bまでしかありません。
7Bや13Bも試すべきなのは間違いない気がしますし、おそらく実験はしたのではないかなと予測できます。ある意味、論文では意図的に3Bまでしか報告しなかったのかなとも思え、ひょっとするとパラメータを増加させると何かしらの別の問題が起こるのかもしれません。
“コスト低下”や”エネルギー効率化”は推論時がメイン。学習時はそうでもない
何度も出てきますが、結局のところここにつきます。
w_quant = w + (weight_quant(w) - w).detach()この後段の計算は効率化されますが、小数型のモデルの重み「w」が逆伝搬のために保持されているため、学習時に必要なGPU使用量が大きく下がるわけではありません。
まだまだ研究余地の多いであることもわかりますね🎇
まとめ
本日はBitNetの解説をしてみました♪
ちょっと難しい内容だったかもしれませんね😅
皆様のかゆいところに手が届く情報になれば嬉しいです!